*본 포스팅은 머신러닝교과서를 참조하여 작성되었습니다.
5.3 커널 PCA를 사용하여 비선형 매핑
실전 애플리케이션에서는 비선형 문제를 더 자주 맞닥뜨린다. 이런 비선형 문제를 다루어야 한다면 PCA와 LDA 같은 차원 축소를 위한 선형 변형 기법은 최선의 선택이 아니다.

5.3.1 커널 함수와 커널 트릭
3장에서 커널 SVM에 관해 배운 것을 떠올려 보면 비선형 문제를 해결하기 위해 클래스가 선형으로 구분되는 새로운 고차원 특성 공간으로 투영할 수 있다.
즉, 커널 PCA를 통한 비선형 매핑을 수행하여 데이터를 고차원 공간으로 변환한다. 그 다음 고차원 공간에 표준 PCA를 사용하여 샘플이 선형 분류기로 구분될 수 있는 저차원 공간으로 데이터를 투영한다. 이 방식의 단점은 계산 비용이 아주 비싸다는 것이다.
여기에 커널 트릭(kernel trick)이 등장한다.
커널 트릭을 사용하면 원본 특성 공간에서 두 고차원 특성 벡터의 유사도를 계산할 수 있다.
기본적으로 커널 함수는 두 벡터 사이의 점곱을 계산할 수 있는 함수이다. 가장 널리 사용되는 커널은 다음과 같다.
- 다항 커널
- 하이퍼볼릭 탄젠트(hyperbolic tangent)(시그모이드(sigmoid))커널
- 방사 기저 함수(Radial Basis Function, RBF)
5.3.2 파이썬으로 커널 PCA 구현
from scipy.spatial.distance import pdist, squareform
from numpy import exp
from scipy.linalg import eigh
import numpy as np
def rbf_kernel_pca(X, gamma, n_components):
"""
RBF 커널 PCA 구현
매개변수
------------------
X : {넘파이 ndarray}, shape = [n_samples, n_features]
gamma : float
RBF 커널 튜닝 매개변수
n_components : int
반환할 주성분 개수
반환값
------------------
X_pc : {넘파이 ndarray}, shape = [n_samples, k_features]
투영된 데이터셋
"""
# MxN 차원의 데이터셋에서 샘플 간의 유클리디안 거리의 제곱을 계산한다.
sq_dists = pdist(X, 'sqeuclidean')
# 샘플 간의 거리를 정방 대칭 행렬로 변환합니다.
mat_sq_dists = squareform(sq_dists)
# 커널 행렬을 계산한다
K = exp(-gamma * mat_sq_dists)
# 커널 행렬을 중앙에 맞춘다
N = K.shape[0]
one_n = np.ones((N, N)) / N
K = K - one_n.dot(K) - K.dot(one_n) + one_n.dot(K).dot(one_n)
# 중앙에 맞춰진 커널 행렬의 고윳값과 고유 벡터를 구한다.
# scipy.linalg.eigh 함수는 오름차순으로 반환한다.
eigvals, eigvecs = eigh(K)
eigvals, eigvecs = eigvals[::-1], eigvecs[:, ::-1]
# 최상위 k개의 고유 벡터를 선택합니다(투영 결과).
X_pc = np.column_stack([eigvecs[:, i] for i in range(n_components)])
return X_pc* 차원 축소에 RBF 커널 PCA를 사용하는 한 가지 단점은 사전에 감마 매개변수를 지정해야 한다는 것이다.
예제 1: 반달 모양 구분하기
rbf_kernel_pca 함수를 빈선형 데이터셋에 적용해 보자. 두 개의 반달 모양을 띤 100개의 샘플로 구성된 2차원 데이터셋을 만들어 보자.
from sklearn.datasets import make_moons
X, y = make_moons(n_samples = 100, random_state = 123)
plt.scatter(X[y==0, 0], X[y==0, 1],
color='red', marker='^', alpha=0.5)
plt.scatter(X[y==1, 0], X[y==1, 1],
color='blue', marker='o', alpha=0.5)
plt.show()
확실히 이 반달 모양 데이터셋은 선형적으로 구분되지 않는다. 우리의 목표는 커널 PCA로 반달 모양을 펼쳐서 선형 분류기에 적합한 입력 데이터셋으로 만드는 것이다. 먼저 기본 PCA의 주성분에 데이터셋을 투영하면 어떻게 보이는지 확인해 보자.
from sklearn.decomposition import PCA
scikit_pca = PCA(n_components=2)
X_spca = scikit_pca.fit_transform(X)
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(7, 3))
ax[0].scatter(X_spca[y==0, 0], X_spca[y==0, 1],
color='red', marker='^', alpha=0.5)
ax[0].scatter(X_spca[y==1, 0], X_spca[y==1, 1],
color='blue', marker='o', alpha=0.5)
ax[1].scatter(X_spca[y==0, 0], np.zeros((50, 1))+0.02,
color='red', marker='^', alpha=0.5)
ax[1].scatter(X_spca[y==1, 0], np.zeros((50, 1))-0.02,
color='blue', marker='o', alpha=0.5)
ax[0].set_xlabel('PC 1')
ax[0].set_ylabel('PC 2')
ax[1].set_ylim([-1, 1])
ax[1].set_yticks([])
ax[1].set_xlabel('PC 1')
plt.show()
이 변환은 동그라미와 삼각형 사이를 판별하는 선형 분류기에 도움이 되지 않는다. 비슷하게 두 개의 반달 모양을 구성하는 동그라미와 삼각형은 오른쪽 그래프처럼 1차원 특성 축에 투영하면 선형적으로 구분이 불가능하다.
이제 앞에서 구현한 커널 PCA 함수 rbf_kernel_pca를 적용해 보자.
X_kpca = rbf_kernel_pca(X, gamma=15, n_components=2)
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(7, 3))
ax[0].scatter(X_kpca[y==0, 0], X_kpca[y==0, 1],
color='red', marker='^', alpha=0.5)
ax[0].scatter(X_kpca[y==1, 0], X_kpca[y==1, 1],
color='blue', marker='o', alpha=0.5)
ax[1].scatter(X_kpca[y==0, 0], np.zeros((50, 1)) + 0.02,
color='red', marker='^', alpha=0.5)
ax[1].scatter(X_kpca[y==1, 0], np.zeros((50, 1)) - 0.02,
color='blue', marker='o', alpha=0.5)
ax[0].set_xlabel('PC1')
ax[0].set_ylabel('PC2')
ax[1].set_ylim([-1, 1])
ax[1].set_yticks([])
ax[1].set_xlabel('PC1')
plt.tight_layout()
plt.show()
이제 두 클래스(동그라미와 삼각형)는 선형적으로 구분이 잘 되므로 선형 분류기를 위한 훈련 데이터로 적합하다.
아쉽지만 여러 가지 데이터셋에 잘 맞는 보편적인 gamma 파라미터 값은 없다. 주어진 문제에 적합한 값을 찾으려면 실험이 필요하다. 여기서는 좋은 결과를 내는 값을 따로 찾아 사용하였다.
예제 2: 동심원 분리하기
from sklearn.datasets import make_circles
X, y = make_circles(n_samples=1000,
random_state=123, noise=0.1, factor=0.2)
plt.scatter(X[y==0, 0], X[y==0, 1],
color='red', marker='^', alpha=0.5)
plt.scatter(X[y==1, 0], X[y==1, 1],
color='blue', marker='o', alpha=0.5)
plt.tight_layout()
plt.show()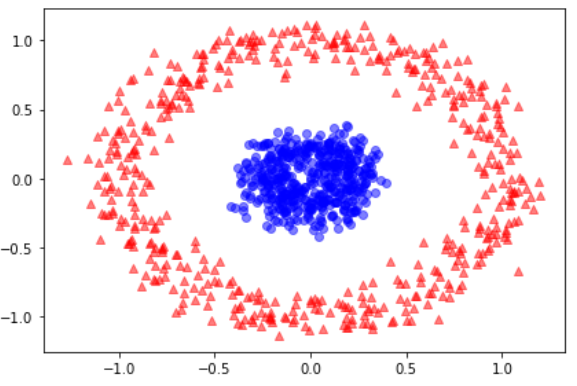
RBF 커널 PCA 결과와 비교하기 위해 먼저 기본 PCA를 적용해 보자.
scikit_pca = PCA(n_components=2)
X_spca = scikit_pca.fit_transform(X)
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(7, 3))
ax[0].scatter(X_spca[y==0, 0], X_spca[y==0, 1],
color='red', marker='^', alpha=0.5)
ax[0].scatter(X_spca[y==1, 0], X_spca[y==1, 1],
color='blue', marker='o', alpha=0.5)
ax[1].scatter(X_spca[y==0, 0], np.zeros((500, 1))+0.02,
color='red', marker='^', alpha=0.5)
ax[1].scatter(X_spca[y==1, 0], np.zeros((500, 1))-0.02,
color='blue', marker='o', alpha=0.5)
ax[0].set_xlabel('PC1')
ax[0].set_ylabel('PC2')
ax[1].set_ylim([-1, 1])
ax[1].set_yticks([])
ax[1].set_xlabel('PC1')
plt.tight_layout()
plt.show()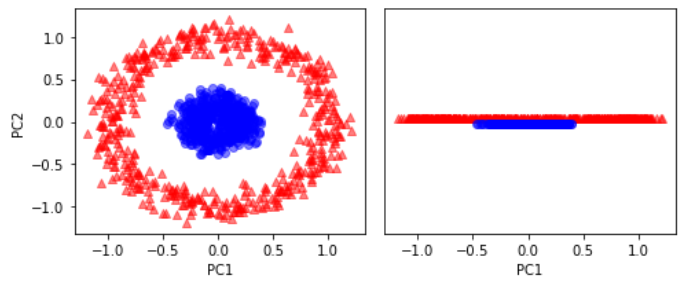
여기서도 기본 PCA는 선형 분류기에 적합한 결과를 만들 수 없다.
적절한 gamma 값을 주고 RBF 커널 PCA 구현을 사용해 보자
X_kpca = rbf_kernel_pca(X, gamma=15, n_components=2)
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(7, 3))
ax[0].scatter(X_kpca[y == 0, 0], X_kpca[y == 0, 1],
color='red', marker='^', alpha=0.5)
ax[0].scatter(X_kpca[y == 1, 0], X_kpca[y == 1, 1],
color='blue', marker='o', alpha=0.5)
ax[1].scatter(X_kpca[y == 0, 0], np.zeros((500, 1)) + 0.02,
color='red', marker='^', alpha=0.5)
ax[1].scatter(X_kpca[y == 1, 0], np.zeros((500, 1)) - 0.02,
color='blue', marker='o', alpha=0.5)
ax[0].set_xlabel('PC1')
ax[0].set_ylabel('PC2')
ax[1].set_ylim([-1, 1])
ax[1].set_yticks([])
ax[1].set_xlabel('PC1')
plt.tight_layout()
plt.show()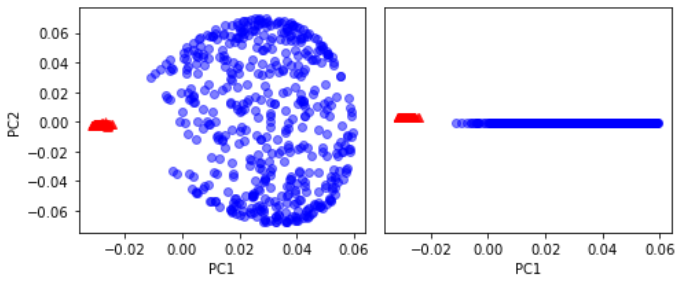
5.3.3 새로운 데이터 포인트 투영
실전에서는 변환해야 할 데이터셋이 하나 이상이다. 예를 들어 훈련 데이터셋과 테스트 데이터셋이다. 모델을 구축하고 평가한 후 수집한 새로운 샘플도 이에 해당한다.
이제 훈련 데이터셋에 포함되지 않았던 새로운 데이터 포인트를 투영하는 방법을 배워보자.
새로운 샘플과 훈련 데이터셋의 샘플 간 유사도를 계산한 후 고윳값으로 고유 벡터를 정규화해야 한다. 앞서 구현한 rbf_kernel_pca 함수를 커널 행렬의 고윳값도 반환하도록 수정한다.
from scipy.spatial.distance import pdist, squareform
from numpy import exp
from scipy.linalg import eigh
import numpy as np
def rbf_kernel_pca(X, gamma, n_components):
"""
RBF 커널 PCA 구현
매개변수
------------
X: {넘파이 ndarray}, shape = [n_samples, n_features]
gamma: float
RBF 커널 튜닝 매개변수
n_components: int
반환할 주성분 개수
Returns
------------
alphas: {넘파이 ndarray}, shape = [n_samples, k_features]
투영된 데이터셋
lambdas: list
고윳값
"""
# MxN 차원의 데이터셋에서 샘플 간의 유클리디안 거리의 제곱을 계산합니다.
sq_dists = pdist(X, 'sqeuclidean')
# 샘플 간의 거리를 정방 대칭 행렬로 변환합니다.
mat_sq_dists = squareform(sq_dists)
# 커널 행렬을 계산합니다.
K = exp(-gamma * mat_sq_dists)
# 커널 행렬을 중앙에 맞춥니다.
N = K.shape[0]
one_n = np.ones((N, N)) / N
K = K - one_n.dot(K) - K.dot(one_n) + one_n.dot(K).dot(one_n)
# 중앙에 맞춰진 커널 행렬의 고윳값과 고유 벡터를 구합니다.
# scipy.linalg.eigh 함수는 오름차순으로 반환합니다.
eigvals, eigvecs = eigh(K)
eigvals, eigvecs = eigvals[::-1], eigvecs[:, ::-1]
# 최상위 k 개의 고유 벡터를 선택합니다(투영 결과).
alphas = np.column_stack([eigvecs[:, i]
for i in range(n_components)])
# 고유 벡터에 상응하는 고윳값을 선택합니다.
lambdas = [eigvals[i] for i in range(n_components)]
return alphas, lambdas
새로운 반달 데이터셋을 만들고 수정된 커널 PCA 구현을 사용하여 1차원 부분 공간에 투영해 보자.
X, y = make_moons(n_samples=100, random_state=123)
alphas, lambdas = rbf_kernel_pca(X, gamma=15, n_components=1)
새로운 샘플을 투영하는 코드를 구현하기 위해 반달 데이터셋의 26번째 포인트가 새로운 데이터 포인트라고 가정하겠다.
x_new = X[25]
x_new
>> array([1.8713, 0.0093])
x_proj = alphas[25] # 원본 투영
x_proj
>> array([0.0788])
def project_x(x_new, X, gamma, alphas, lambdas):
pair_dist = np.array([np.sum((x_new - row)**2) for row in X])
k = np.exp(-gamma * pair_dist)
return k.dot(alphas / lambdas)project_x 함수를 사용하면 새로운 데이터 샘플도 투영할 수 있다.
# 새로운 데이터포인트를 투영합니다.
x_reproj = project_x(x_new, X, gamma=15, alphas=alphas, lambdas=lambdas)
x_reproj
>> array([0.0788])
이제 첫 번째 주성분에 투영한 것을 그래프로 그려보자
plt.scatter(alphas[y == 0, 0], np.zeros((50)),
color='red', marker='^', alpha=0.5)
plt.scatter(alphas[y == 1, 0], np.zeros((50)),
color='blue', marker='o', alpha=0.5)
plt.scatter(x_proj, 0, color='black',
label='Original projection of point X[25]', marker='^', s=100)
plt.scatter(x_reproj, 0, color='green',
label='Remapped point X[25]', marker='x', s=500)
plt.yticks([], [])
plt.legend(scatterpoints=1)
plt.tight_layout()
# plt.savefig('images/05_18.png', dpi=300)
plt.show()
위 산점도에서 볼 수 있듯 샘플이 첫 번째 주성분에 올바르게 매핑되었다.
5.3.4 사이킷런의 커널 PCA
from sklearn.decomposition import KernelPCA
X, y = make_moons(n_samples=100, random_state=123)
scikit_kpca = KernelPCA(n_components=2,
kernel='rbf', gamma=15)
X_skernpca = scikit_kpca.fit_transform(X)
우리가 구현한 커널 PCA와 동일한 결과가 나오는지 확인하기 위해 변환된 반달 모양 데이터를 처음 두 개의 주성분에 그려 보겠다.
plt.scatter(X_skernpca[y == 0, 0], X_skernpca[y == 0, 1],
color='red', marker='^', alpha=0.5)
plt.scatter(X_skernpca[y == 1, 0], X_skernpca[y == 1, 1],
color='blue', marker='o', alpha=0.5)
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.tight_layout()
# plt.savefig('images/05_19.png', dpi=300)
plt.show()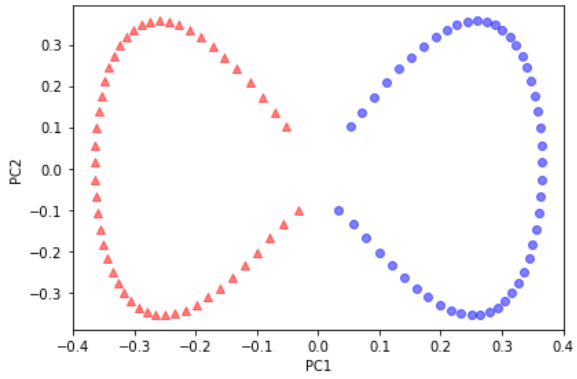
사이킷런의 KernelPCA 결과는 직접 구현한 것과 같다.
5.4 요약
- 특성 추출을 위한 세 개의 기본적인 차원 축소 기법을 배웠다. 기본 PCA, LDA, 커널 PCA
- PCA는 클래스 레이블을 사용하지 않고 직교하는 특성 축을 따라 분산이 최대가 되는 저차원 부분 공간으로 데이터를 투영한다.
- PCA와 다르게 LDA는 지도 학습 방법의 차원 축소 기법이다. 훈련 데이터셋에 있는 클래스 정보를 사용하여 선형 특성 공간에서 클래스 구분 능력을 최대화한다.
- 비선형 특성 추출 방법인 커널 PCA를 배웠다. 커널 트릭과 고차원 특성 공간으로서의 가상 투영을 통하혀 비선형 특성을 가진 데이터셋을 저차원 부분 공간으로 극적으로 압축한다. 이 부분 공간에서 클래스는 선형적으로 분리될 수 있다.
'소소하지만 소소하지 않은 개발 공부 > 머신 러닝 교과서' 카테고리의 다른 글
| 7. 다양한 모델을 결합한 앙상블 학습, 머신러닝교과서, python (0) | 2022.12.19 |
|---|---|
| 6.2 k-겹 교차 검증을 사용한 모델 성능 평가 (0) | 2022.12.14 |
| 5.차원 축소를 사용한 데이터 압축, 머신러닝교과서, python (1) | 2022.12.11 |
| 4.6 랜덤 포레스트의 특성 중요도 사용, 머신러닝교과서, python (0) | 2022.12.07 |
| Chapter3.7 k-최근접 이웃: 게으른 학습 알고리즘, 머신러닝교과서, python (1) | 2022.11.29 |