* 본 포스팅은 머신러닝교과서를 참조하여 작성되었습니다.
5.1 주성분 분석을 통한 비지도 차원 축소
특성 선택 vs 특성 추출
- 원본 특성을 유지한다면 특성 선택
- 새로운 특성 공간으로 데이터를 변환하거나 투영한다면 특성 추출
특성 추출은 대부분의 관련 있는 정보를 유지하면서 데이터를 압축하는 방법이다. 이는 저장 공간을 절약하거나 학습 알고리즘의 계산 효율성을 향상시키고 차원의 저주(curse of dimensionality) 문제를 감소시켜 예측 성능을 향상시키기도 한다.
5.1.1 주성분 분석의 주요 단계
PCA : 비지도 선형 변환 기법
PCA를 많이 사용하는 애플리케이션에는 탐색적 데이터 분석과 주식 거래 시장의 잡음 제거, 생물정보학 분야에서 게놈(genome) 데이터나 유전자 발현(gene expression) 분석 등이 있다.
PCA는 특성 사이의 상관관계를 기반으로 하여 데이터에 있는 패턴을 찾을 수 있다. 즉 고차원 데이터에서 분산이 가장 큰 방향을 찾고 좀 더 작거나 같은 수의 차원을 갖는 새로운 부분 공간으로 이를 투영한다.
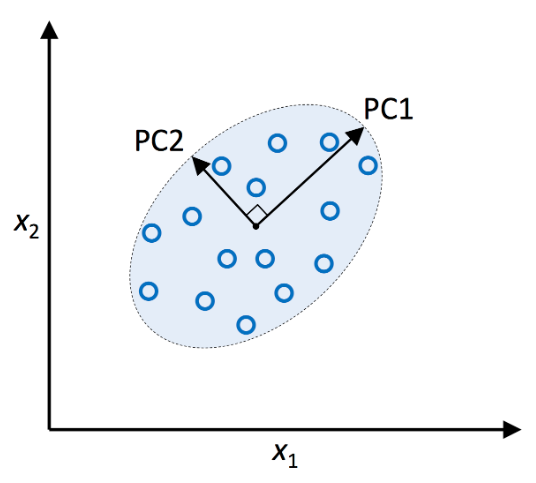
- 새로운 부분 공간의 직교 좌표(주성분)는 주어진 조건하에서 분산이 최대인 방향으로 해석할 수 있다.
- 새로운 특성 축은 위 그림과 같이 서로 직각을 이룬다.
- x1,x2 는 원본 특성 축
- PC1, PC2는 주성분
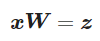
차원 축소를 위한 PCA 알고리즘을 자세히 알아보기 전에 사용할 방법을 몇 단계로 나눠보자.
- d차원 데이터셋을 표준화 전처리한다.
- 공분산 행렬(covariance matrix)을 만든다.
- 공분산 행렬을 고유 벡터(eigenvector)와 고윳값(eigenvalue)으로 분해한다.
- 고윳값을 내림차순으로 정렬하고 그에 해당하는 고유 벡터의 순위를 매긴다.
- 고윳값이 가장 큰 k개의 고유 벡터를 선택한다. 여기서 k는 새로운 특성 부분 공간의 차원이다.(k <= d).
- 최상위 k개의 고유 벡터로 투영 행렬(projection matrix) W를 만든다.
- 투영 행렬 W를 사용해서 d 차원 입력 데이터셋 X를 새로운 k차원의 특성 부분 공간으로 변환한다.
5.1.2 주성분 추출 단계
파이썬으로 PCA를 하나씩 구현해 보자.
PCA 처음 네 단계
- 데이터를 표준화 전처리한다.
- 공분산 행렬을 구성한다.
- 공분산 행렬의 고윳값과 고유 벡터를 구한다
- 고윳값을 내림차순으로 정렬하여 고유 벡터의 순위를 매긴다.
import pandas as pd
df_wine = pd.read_csv('https://archive.ics.uci.edu/ml/'
'machine-learning-databases/wine/wine.data',
header=None)
from sklearn.model_selection import train_test_split
X,y = df_wine.iloc[:, 1:].values, df_wine.iloc[:,0].values
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, stratify=y, random_state=0)
# 특성을 표준화 전처리한다.
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train_std = sc.fit_transform(X_train)
X_test_std = sc.transform(X_test)
# 공분산 행렬의 고윳값 분해
import numpy as np
cov_mat = np.cov(X_train_std.T)
eigen_vals, eigen_vecs = np.linalg.eig(cov_mat)
print('\n 고윳값 \n%s' % eigen_vals)
>> [4.84274532 2.41602459 1.54845825 0.96120438 0.84166161 0.6620634
0.51828472 0.34650377 0.3131368 0.10754642 0.21357215 0.15362835
0.1808613 ]
5.1.3 총 분산과 설명된 분산
데이터셋 차원을 새로운 특성 부분 공간으로 압축하여 줄여야 하기에 가장 많은 정보(분산)를 가진 고유 벡터(주성분) 일부만 선택한다. 고윳값은 고유 벡터의 크기를 결정하므로 고윳값을 내림차순으로 정렬한다. 고윳값 순서에 따라 최상위 k개의 고유 벡터를 선택한다. 가장 정보가 많은 k개의 고유 벡터를 선택하기 전에 고윳값의 설명된 분산 비율(explained variance ratio)을 그래프로 그려보자.
tot = sum(eigen_vals)
var_exp = [(i / tot) for i in sorted(eigen_vals, reverse=True)]
cum_var_exp = np.cumsum(var_exp)
import matplotlib.pyplot as plt
plt.bar(range(1, 14), var_exp, alpha = 0.5, align='center', label= 'Individual explained variance')
plt.step(range(1, 14), cum_var_exp, where='mid', label = 'Cumulative explained variance')
plt.ylabel('Explained variance ratio')
plt.xlabel('Principal component index')
plt.legend(loc='best')
plt.tight_layout()
plt.show()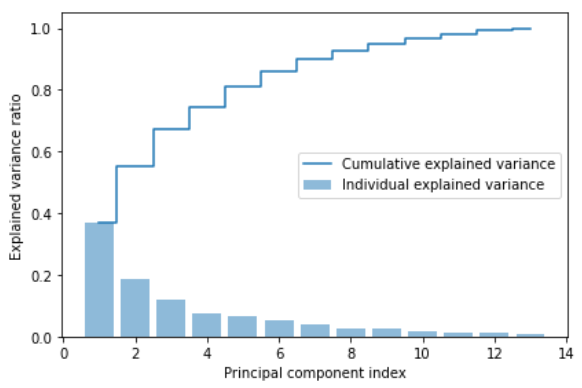
- 결과 그래프는 첫 번째 주성분이 거의 분산의 40%를 커버하고 있음을 보여준다.
- 처음 두 개의 주성분이 데이터셋에 있는 분산의 대략 60% 를 설명한다.
설명된 분산 그래프가 4장에서 랜덤 포레스트로 계산한 특성 중요도를 떠올리게 하지만 PCA는 비지도 학습이다. 클래스 레이블에 관한 정보는 사용하지 않았다. 랜덤 포레스트는 클래스 소속 정보를 사용하여 노드의 불순도를 계산하는 반면, 분산은 특성 축을 따라 값들이 퍼진 정도를 측정한다.
5.1.4 특성 변환
공분산 행렬을 고유 벡터와 고윳값 쌍으로 성공적으로 분해한 후 wine 데이터셋을 새로운 주성분 축으로 변환하는 나머지 세 단계를 진행해 보자.
- 고윳값이 가장 큰 k개의 고유 벡터를 선택한다. 여기서 k는 새로운 특성 부분 공간의 차원이다.
- 최상위 k개의 고유 벡터로 투영 행렬 W를 만든다.
- 투영 행렬 W를 사용해서 d차원 입려 데이터셋 X를 새로운 k차원의 특성 부분 공간으로 변환한다.
# (고윳값, 고유 벡터) 튜플의 리스트를 만든다
eigen_pairs = [(np.abs(eigen_vals[i]), eigen_vecs[:, i])
for i in range(len(eigen_vals))]
# 높은 값에서 낮은 값으로(고윳값, 고유 벡터) 튜플을 정렬한다.
eigen_pairs.sort(key=lambda k : k[0], reverse=True)
w = np.hstack((eigen_pairs[0][1][:, np.newaxis],
eigen_pairs[1][1][:, np.newaxis]))
print('투영 행렬 W:\n', w)
>> 투영 행렬 W:
[[-0.13724218 0.50303478]
[ 0.24724326 0.16487119]
[-0.02545159 0.24456476]
[ 0.20694508 -0.11352904]
[-0.15436582 0.28974518]
[-0.39376952 0.05080104]
[-0.41735106 -0.02287338]
[ 0.30572896 0.09048885]
[-0.30668347 0.00835233]
[ 0.07554066 0.54977581]
[-0.32613263 -0.20716433]
[-0.36861022 -0.24902536]
[-0.29669651 0.38022942]]X_train_std[0].dot(w)
>> array([2.38299011, 0.45458499])비슷하게 전체 124 x 13 차원의 훈련 데이터셋을 행렬 점곱으로 두 개의 주성분에 투영할 수 있다.
X_train_pca = X_train_std.dot(w)
colors = ['r', 'b', 'g']
markers = ['s', 'x', 'o']
for l, c, m in zip(np.unique(y_train), colors, markers):
plt.scatter(X_train_pca[y_train == l, 0],
X_train_pca[y_train == l, 1],
c = c, label = l, marker=m)
plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.legend(loc = 'lower left')
plt.tight_layout()
plt.show()
- 결과 그래프에서 볼 수 있듯 데이터가 y축(두 번째 주성분)보다 x축(첫 번째 주성분)을 따라 더 넓게 퍼져 있다.
- 이전 절에서 만든 설명된 분산의 그래프와 동일한 결과이다. 즉, 선형 분류기가 클래스들을 잘 분리할 수 있을 것 같다고 직관적으로 알 수 있다.
5.1.5 사이킷런의 주성분 분석
from matplotlib.colors import ListedColormap
def plot_decision_regions(X, y, classifier, resolution=0.02):
# 마커와 컬러맵을 준비한다
marker = ('s', 'x', 'o', '^', 'v')
colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
cmap = ListedColormap(colors[:len(np.unique(y))])
# 결정 경계를 그린다
x1_min, x1_max = X[:, 0].min() -1, X[:,0].max() + 1
x2_min, x2_max = X[:, 1].min() -1, X[:,1].max() + 1
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
np.arange(x2_min, x2_max, resolution))
Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
Z = Z.reshape(xx1.shape)
plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
# 클래스 샘플을 표시한다.
for idx, cl in enumerate(np.unique(y)):
plt.scatter(x=X[y == cl, 0],
y=X[y == cl, 1],
alpha = 0.6,
c=cmap.colors[idx],
edgecolor='black',
marker = markers[idx],
label = cl)
from sklearn.linear_model import LogisticRegression
from sklearn.decomposition import PCA
# PCA 변환기와 로지스틱 회귀 추정기를 초기화한다
pca = PCA(n_components=2)
lr = LogisticRegression(random_state = 1)
# 차원 축소
X_train_pca = pca.fit_transform(X_train_std)
X_test_pca = pca.transform(X_test_std)
#축소된 데이터셋으로 로지스틱 회귀 모델 훈련
lr.fit(X_train_pca, y_train)
plot_decision_regions(X_train_pca, y_train, classifier=lr)
plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.legend(loc='lower left')
plt.tight_layout()
plt.show()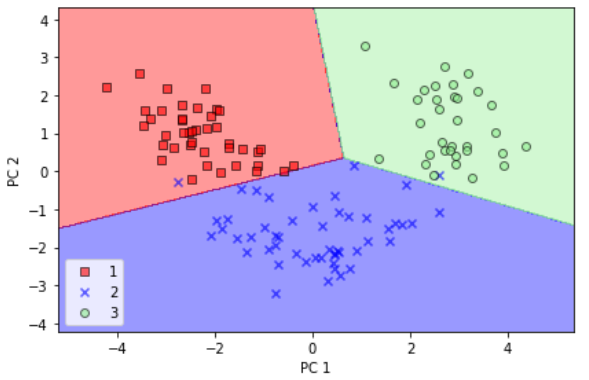
예제를 맘리하기 위해 테스트 데이터셋을 변환하고 로지스틱 회귀가 클래스를 잘 구분하는지 결정 경계를 그려보자.
plot_decision_regions(X_test_pca, y_test, classifier=lr)
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.legend(loc='lower left')
plt.tight_layout()
plt.show()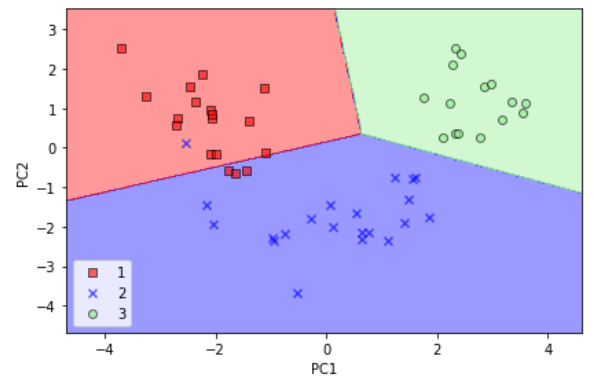
- 데이트 데이터셋에서 결정 결계를 그리고 나면 로지스틱 회귀가 2차원 특성 부분 공간에서 매우 잘 작동한다는 것을 알 수 있다. 테스트 데이터셋에 있는 샘풀 몇개만 분류하지 못했다.
전체 주성분의 설명된 분산 비율을 알고 싶다면 n_compoents 매개변수를 None 으로 저장하고 PCA 클래스의 객체를 만들면 된다.
pca = PCA(n_components=None)
X_train_pca = pca.fit_transform(X_train_std)
pca.explained_variance_ratio_
>> array([0.36951469, 0.18434927, 0.11815159, 0.07334252, 0.06422108,
0.05051724, 0.03954654, 0.02643918, 0.02389319, 0.01629614,
0.01380021, 0.01172226, 0.00820609])
'소소하지만 소소하지 않은 개발 공부 > 머신 러닝 교과서' 카테고리의 다른 글
| 6.2 k-겹 교차 검증을 사용한 모델 성능 평가 (0) | 2022.12.14 |
|---|---|
| 5.3 커널 PCA를 사용하여 비선형 매핑, 머신러닝교과서, python (0) | 2022.12.13 |
| 4.6 랜덤 포레스트의 특성 중요도 사용, 머신러닝교과서, python (0) | 2022.12.07 |
| Chapter3.7 k-최근접 이웃: 게으른 학습 알고리즘, 머신러닝교과서, python (1) | 2022.11.29 |
| Chapter 3.6 결정 트리 학습, 머신러닝교과서, pyhon (0) | 2022.11.29 |